كتبت هذه المقالة على شرف والتر رويدن
في العام 2010، تم قبول طلبي للإلتحاق في جامعة ويسكنسون في مدينة ماديسون في نفس الوقت الذي فقد فيه المجتمع الرياضي واحد من أعظم الرياضيين الذين أثروا في مسار التحليل الرياضي و أصدروا أعظم الكتب فيها.
كنت أحمل كتب والتر رودين أينما ذهبت وكنت راغبة كل الرغبة بالفهم العميق لهذين الكتابين اللذان يعتبران كحجري الأساس لطالب التحليل الحقيقي. كانت مقابلتي عندئذ تتضمن أسئلة عن والتر رودين وماأعرف عنه وعن أعماله. فقمت بشرح كيف عرفته من خلال كتبه ولم أعرف عنه شيئاً في الوقت نفسه.
كان والتر رودين بروفيسور متقاعد من جامعة ويسكنسون، وتوفي في منزله في 20 مايو بعد صراع طويل مع مرض باركنسون عن عمر يناهز 89 عاماً.
ينحدر رودين من أسرة يهودية عريقة عرفت في الثلث الأول من القرن التاسع عشر. في العام 1830، كان جد والتر رودين الأكبر آرون بولاك يملك مصنع لصنع أعواد الثقاب و أصبح أيضاً معروفاً بكثرة أعماله الخيرية منها بناء مجمع سكني للطلاب حيث أقام 75 طالب من جامعة فيينا التقنية من دون دفع أي مال وعلى إثر ذلك تم منحه وسام الفروسية في العام 1869 و إختار الإسم فون رودين.
وبذلك كان والد والتر رودين، روبرت، الإبن الثالث لفون بدلاك، مالك مصنع ومهندس كهربائي حاصل على شهادة الدكتوراة في الهندسة الكهربائية من جامعة فيينا التقنية في يونيو 1914 و مخترعاً مهتماً بالتسجيلات الصوتية و تكنولوجيا الراديو. وقد تزوج من والدة والتر، ناتالي، في العام 1920. ولد والتر في العام 1921 في فيينا وهو أكبر طفلين لوالديه، ولديه أخت صغيرة فيرا ولدت في 31 مايو 1925. وكانت العائلة اليهودية يهودية، لكنهم لم يكونوا متدينين.
لم يلتحق والتر بالروضة لكنه إلتحق بمدرسة إبتدائية لمدو 4 سنوات ثم إلتحق بنفس المدرسة التي إلتحق بها والده وجده في فيينا و التي وصفها والتر بنفسه كالتالي:
...كانت على مسافة قريبة من شقتنا. اضطررت لإجراء إمتحان القبول، و الذي لم يكن مشكلة. كان لدينا 5 فصول كل يوم، من الساعة 8 إلى 1، مع إستراحة لمدة 20 دقيقة في منتصف الصباح، حيث كان بإمكاننا الركض حول ساحة الحصى أو لعب بعض الألعاب هناك. كنا نلتقي في الدرسة 6 أيام في الأسبوع. كان جميع الطلاب و المعلمين من الذكور. أعتقد أن الإناث الوحيدات اللائي دخلن المبنى كن أمهات في ليالي الذهاب إلى المدرسة. كان هناك حوالي 20 أو 25 صبياً في صفي، و بقينا من عام إلى آخر. بقينا في غرفة واحدة، وتناوب المعلمون على الحضور. كانوا كلهم يحملون شهادة الدكتوراة و جميعهم يلقب بالبرفسور. كان قد تم وضع المنهج مسبقاً. لم يكن هناك خيار للتغيير، بإستثناء أنه يمكن إضافة مواد إختيارية إلى ماهو مطلوب.
كانت الثلاثينيات من القرن الماضي أوقات حرب عصيبة لأولئك المنحدرين من أصول يهودية في فيينا حيث تزايدت الهجمات على اليهود. كانت سياسات النازيين في ألمانيا بعد وصول هتلر إلى السلطة في عام 1933 مصدر قلق بالغ حيث كان هناك العديد من المتعاطفين مع النازيين في فيينا. ومع ذلك، وصلت هذه المخاوف
إلى مستوى مختلف تماما 12 مارس .1938 وفي ً عندما زحفت القوات الألمانية إلى النمسا و ضمتها في
اليوم الثالي، تم مضايقة اليهود في فيينا، و تعرضت منازلهم و متاجرهم للهجوم. أرسل والدا والتر على الفور
والتر وشقيقته فيرا إلى سويسرا لمواصلة تعليمهما. وصلوا إلى زوريخ ومن هناك ذهبت فيرا إلى
Chexbres حيث إلتحقت بمدرسة داخلية للبنات بينما ذهب والتر إلى معهد Rosenberg dem auf للبنين
في Gallen St . وبقلم رودين:
إلتحقت في المعهد ببرنامج خاص صغير و الذي كان يدرب الطلاب لإختبار يعقد من قبل جامعة أكسفورد
وهو يعطى في الكثير من الأماكن حول العالم.
بعد ستة أشهر إنضم والدا والتر إلى إبنيهما في سويسرا، كان عليهما أن يغادرا فيينا من دون أن يأخذا أي شئ
معهما سوى ملابسهما اللاتي يؤتديانها. وظنا أنهما سوف يبقيان هناك لكن سرعان ماعرفا أنه يجب أيضاً
إلى فرنسا حيث حصل الأب روبرت على عمل هناك
مغادرة سويسرا في أسرع وقت ممكن فإنتقلوا جميعاً
بمساعدة صديق له لكن كان عليهم أن يجددوا إقامتهم في الشرطة بين حين وآخر. ومع إنلاع الحرب العالمية
الثانية ،1939 لم يكن الفرنسيون سعداء بوجود الألمان بينهم فإعتقل والتر و أبوه و إرسلوا إلى المعسكر
ميسلاي دو مين. وبعد نقله لعدة معسكرات، إستدعي والتر للخدمة في الجيش الفرنسي، و أرسل إلى بونتيفي.
توقف القتال. أخبر الفرنسيون والتر بأن
لكن بحلول هذا الوقت، كان الألمان قد غزوا فرنسا وبعدها سريعاً
إلى إنجلترا في
عليه الهرب وهذا مافعله حيث هرب إلى الجنوب الغربي من فرنسا. ومن هناك إستقل قارباً
للأجانب.
20 نوفمبر من العام .1940 كان هذه هو الجزء الوحيد من الجيش البريطاني الذي كان مفتوحاً
قضى رودين سنوات الحرب في إنجلترا. وقرب نهية الحرب، أعلنت البحرية الملكية أنها بحاجة إلى
مترجمين فوريين، ويفضل أن يكونوا متحدثين أصليين للألمانية. بعد التقديم و الخضع للإختبارات في لندن،
وفي 4 فبراير 1944 انضم رودن إلى البحرية الملكية.
في يناير،1945 حصل على إذن للسفر إلى أفينيون حيث يعيش والديهو أخته. عاد إلى إنجلترا، لكن بقية أفراد
عائلته تمكنوا من الهجرة إلى الولايات المتحدة بعد إنتهاء الحرب. انتقلت أخته فيرا إلى دور هام بولاية نورث
كارولينا، حيث عملت في الكيمياء في جامعة ديوك. تمكن والتر روبين من الإنضمام إلى بقية عائلته في
الولايات المتحدة في نهاية عام 1045 بعد انتهاء الحرب. التحق بشقيقته في دور هام بولاية نورث كارولينا.
لم يكن رودن قد إلتحق بأي تعليم بعد المدرسة لكنه تكلم مع الأعضاء من قسم الرياضيات في جامعة ديوك و
أقتعهم بقدرته على الإنضمام و الحصول على البكالوريوس منها. وبالفعل حصل والتر رودن على
البكالوريوس من جامعة ديوك في العام .1947
لجربفبن كومارد إيفانز و
أجرى بحثه بعد ذلك تحت إشراف الدكتور جون جاي جرجين و الذي كان طالباً
سزولم ماندلبورت، فحصل على درجة الدكتوراة في الرياضيات في العام 1949 برسالته" نظرية الوحدانية
لمتسلسلات لابلاس" . و التي منها نشر مباشرة ورقتين بحثيتين. الجزء الأول من الرسالة نشر في العام
1950 في الورقة " التمثيل التكاملي للدوال المتصلة" . أما الجزء الثاني من الرسالة فقد نشر في ورقة بحثية
بنفس مسمى الرسالة.
عرض عليه جيرغن التدريس للفترة 1950-1949 في جامعة ديوك 12 ساعة في الأسبوع وقد قبل. خلال
هذا العام في جامعة ديوك، التقى رودن ماري إلين استيل التي حصلت على درجة الدكتوراة من جامعة
تكساس في عام 1949 ثم تم تعيينها كمدرسة في الرياضيات في جامعة ديوك.
غادر رودن جامعة ديوك في العام 1950 ثم شغل منصب مدرس في معهد ماساشوستس للتقنية. خلال هذه
الفترة أنهى مسودة كتابه Analysis Mathematical in Principles في ربيع عام .1952 وقد نشر
الكتاب في العام .1953 وعين في العام 1952 برفسور في جامعة روشستر.
تزوج والتر رودن من ماري في أغسطس من العام 1953 في هيوستن وقد أنجبا أربعة أولاد: كاثرين،
إلينور، روبرت و شارلز.
في العام 1958 ، مكنت زمالة سلون والتر من قضاء بعض الوقت في جامعة ييل. في ذلك الوقت تمت
بالتدريس في الصيف لكنه
مكالمته من قبل Bing.H.R من جامعة ويسكنسون-ماديسون لسؤاله إذا كان مهتماً
رفض ذلك. ثم تم تعيينه أستاذا -ماديسون في عام .1959 وتم تكريمه فيما بعد بتعيينه ً في جامعة ميسكنسون
في منصب أستاذية فيلاس، وهو أرقى أساتذة الجامعة للإنجاز العلمي و النهوض بالتعليم. وظل هناك حتى
تقاعده في عام 1991 و أصبح أستاذاً فخرياً في ذلك الوقت.
كان والتر رودن و زوجته أحد أبرز علماء الرياضيات في عصره وعمل في مختلف مجالات التحليل
الرياضي آنذاك وقدم مساهمات كبيرة في كل منها. عكست أعماله المبكرة التدريب الكلاسيكي له و ركز فيها
بالدراسات الجديدة في فضاء
على دراسة المتسلسلات المثلثية و الدوال التحليلة في متغير واحد. وتأثر أيضاً
باناخ و جبر الدوال. واحدة من أهم نتائجه في هذا المجال، و التي كانت بنا ًء على أعمال Beurling Arne ،
وهي التوصيف الكامل للمثاليات المغلقة في جبر القرص في العام .1956
أيضا،ً أحد أهم المجالات التي إهتم بها رودن كانت في النظرية العامة في التحليل التوافقي على المجموعات
الإبدالية المتراصة محليا 1950 و 1960 كان هذا المجال من المجالات الشهيرة و النشطو للغاية ً في أواخر
في البحث لدرجة أن والتر إقترح أن يتم تقديم الإختصار “lgbalcag “بدلاً من locally a be G Let
group Abelian compact والتي هي لتكن G زمرة إبدالية متراصة محلياً حيث أن هذه العبارة بدأت بها
جميع ندوات التحليل الرياضي في ذلك الوقت. أحد أهم إنجازات والتر في هذا المجال كان في العام 1959
بالتعاون مع Katznelsop and ,Kahane ,Helson في توصيف الدوال التي تعمل على تحويلات فورير
على جبر 1L . ثم قام والتر بتجميع جميع النتائج التي توصلوا إليها في كتابة تحويلات فورير على الزمر.
في نهاية ،1960 تغيرت مرة أخرى إهتمامات والتر وبدأ بالعمل على مسائل التحليل المركب في عدة
متغيرات. كان هذا من المجالات الجديدة و الغير مستكشفة في ذلك الوقت لدرجة لم يكن واضحاً حتى ماهو
التعميم الصحيح لعدة متغيرات من أحادي البعد على قرص الوحدة. هناك إحتمالان على الأقل: الأقراص
المتعددة أو الكرة. فقام والتر بإستكشاف كليهما. فعلى سبيل المثال، فقد أثبت على الأقراص المتعددة 1967 و
على كرة الوحدة 1976 بأن المجموعات الصفرية على فئات p^H المختلفة للدوال تكون مختلفة. كان عمله
في " conjecture function inner " أدى إلى كم هائل من الأبحاث. وبعد حلها من قبل Aleksandrov
Low-Sibony-Hakim and ، قدم والتر مساهمات إضافية هامة لهذا السؤال. أغلب أعمال رودن في
عدة متغيرات مركبة تم عرضها في ثلاثة كتب من كتبه في الرياضيات المتقدمة. الأول نشر في العام 1969
في نظرية الدوال على متعدد الأقراص. و الثاني نشر في العام 1980 وهو نظرية الدوال على كرة الوحدة.
أما عمله على functions inner فتم تلخيصه في سلسلة محاضرات CBMS-NDF ، و التي نشرت بعد
ذلك في العام .1986
عرف والتر رودن لأجيال من طلاب البكالوريوس وطلاب الدرسات العليا من خلال ثلاثة من الكتب
Principles of Mathematical analysis (1953) Real and Complex analysis :المتميزة
(1973) analysis Functional and) 1966 (. وقد حصل على جائزة الجمعية الرياضية الأمريكية
للعرض الرياضي. وحصل على الدرجة الفخرية من جامعة فيينا في العام 2006 .




 ، يوجد فقط شكل واحد من
، يوجد فقط شكل واحد من 


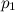 و
و 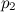 معطاه، فإن هناك طي وحيد للورقة ليمر خلال النقطتين.
معطاه، فإن هناك طي وحيد للورقة ليمر خلال النقطتين. 

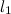 و
و 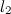 ، فهناك طي لينطبق
، فهناك طي لينطبق 



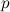 و مستقيمين
و مستقيمين 

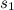 وله الحجم
وله الحجم 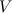 . مهمتك هي إيجاد طول الضلع
. مهمتك هي إيجاد طول الضلع 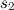 للمكعب الذي حجمه
للمكعب الذي حجمه 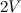 .
. 
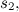 ،وهكذا يكون
،وهكذا يكون ![\[ s_2^3=2V, \]](http://plus.maths.org/MI/ae1582feb52be032e5c34da74b9d3c19/images/img-0002.png)
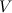 هو الحجم المعطى للمكعب. بما أن
هو الحجم المعطى للمكعب. بما أن 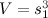 حيث
حيث 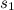 هو طول الضلع المعطى للمكعب، يكون لدينا
هو طول الضلع المعطى للمكعب، يكون لدينا ![\[ s_2^3=2s_1^3, \]](http://plus.maths.org/MI/ae1582feb52be032e5c34da74b9d3c19/images/img-0006.png)
![\[ s_2=\sqrt [3]{2}s_1. \]](http://plus.maths.org/MI/ae1582feb52be032e5c34da74b9d3c19/images/img-0007.png)
![$\sqrt [3]{2}$](http://plus.maths.org/MI/ae1582feb52be032e5c34da74b9d3c19/images/img-0008.png) هو الذي تحتاجه. وهذا هو الذي أوجدناه بالضبط في البناء العلوي.
هو الذي تحتاجه. وهذا هو الذي أوجدناه بالضبط في البناء العلوي. 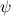 يمكن تقسيمها إلى ثلاثة أقسام بإستخدام علم المثلثات: بكتابة
يمكن تقسيمها إلى ثلاثة أقسام بإستخدام علم المثلثات: بكتابة 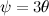 وتطبيق الصيغة المثلثية لجيب تمام مجموع الزاويتين، نحصل على
وتطبيق الصيغة المثلثية لجيب تمام مجموع الزاويتين، نحصل على ![\[ \cos (\psi )=\cos (\theta + 2\theta ) = \cos (\theta )\cos (2\theta )-\sin (\theta )\sin (2\theta ). \]](http://plus.maths.org/MI/339d03bac66caaf6cbd6ece3a356fe65/images/img-0003.png)
![\[ \cos (2\theta )=\cos (\theta )^2-\sin (\theta )^2 \]](http://plus.maths.org/MI/339d03bac66caaf6cbd6ece3a356fe65/images/img-0004.png)
![\[ \cos (3\theta ) = 4\cos (\theta )^3-3\cos (\theta ). \]](http://plus.maths.org/MI/339d03bac66caaf6cbd6ece3a356fe65/images/img-0006.png)
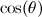 والتي من خلالها يمكن إيجاد
والتي من خلالها يمكن إيجاد 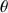 .
. ![\[ ax^3+bx^2+cx+d=0, \]](http://plus.maths.org/MI/cf014aa9770f8622746b75d77ae77d8b/images/img-0001.png)
 و
و 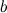 و
و  و
و 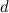 (يمكنك معرفة كيف يمكن عمل ذلك على الموقع الإلكتروني كاشيروا هاتوري) وفي حين أن طريقة إقليدس يمكنها حل المعادلة التربيعية هندسياً فقط بإستخدام الحافة المستقيمة و البوصلة فلا يمكنها حل المعادلة التكعيبية.
(يمكنك معرفة كيف يمكن عمل ذلك على الموقع الإلكتروني كاشيروا هاتوري) وفي حين أن طريقة إقليدس يمكنها حل المعادلة التربيعية هندسياً فقط بإستخدام الحافة المستقيمة و البوصلة فلا يمكنها حل المعادلة التكعيبية. 


